什么是二分查找
二分查找,也叫折半查找,是一种采用一分为二的策略来缩小查找范围并快速靠近目标的算法,不过它要求查找的数据必须是有序排列的。二分查找的基本实现是:
假设数组中的元素是从小到大排列的,以数组的中间位置将数组一分为二,再将数组中间位置的元素与目标数据进行比较。如果它比目标数据大,则在数组的前半部分重复这个查找过程;如果它比目标数据小,则在数组是的后半部分查找;如果它正好等于目标数据,则查找成功。重复上述过程,直到找到目标数据为止;或者在数组不能一分为二时,则查找失败。

采用二分查找算法时,需要计算中间位置,用它将查找范围一分为二,不断靠近目标。中间位置的计算公式为:
中间位置 =(结束位置 - 起始位置 )/ 2 + 起始位置注意:当计算结果为小数时,需要四舍五入,确保结果是一个整数。
二分查找过程详解
为了让你更好的理解二分查找,下面将使用扑克牌来演示二分查找算法的具体过程。
准备扑克纸牌一副,红色棋子一枚。去牌面为2、4、6、7、8的5张纸牌进行排序操作。由于二分查找算法需要确保数据是有序排列的,我们可以使用之前介绍的排序算法将牌面进行排序,排序后的牌面从左到右依次为2、4、6、7、8。
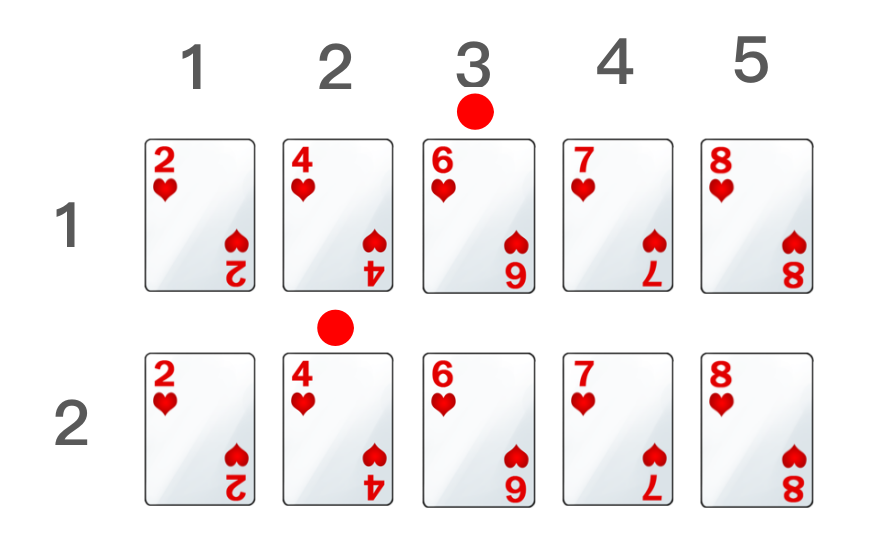
假定要查找的纸牌为4,其具体步骤如下:
第一次查找:起始位置为1,结束位置为5,则中间位置 = (5 – 1)/ 2 + 1 = 3,将红色棋子放在第3张纸牌上方,此时对应的纸牌为6,说明目标纸牌4应该在纸牌6的左边。
第二次查找:起始位置为1,结束位置为3,则中间位置 = (3 – 1)/ 2 + 1 = 2,将红色棋子放在第2张纸牌上方,此时对应的纸牌为4,和我们的查找目标一致,返回纸牌的位置,整个查找过程就结束了。
查找过程如图所示:
编程思路
根据上面的分析,二分查找算法用到了分治策略,因此需要使用递归来实现,可以定义一个自制积木,命名为“二分查找”,然后在自制积木中,根据条件再次调用自己。
其次,在每次查找的过程中,都需要根据起始位置和结束位置来计算中间位置,如果找到了,则直接结束程序,如果找遍所有的位置,都没有找到,可以返回数字0,表示查找失败。
程序实现
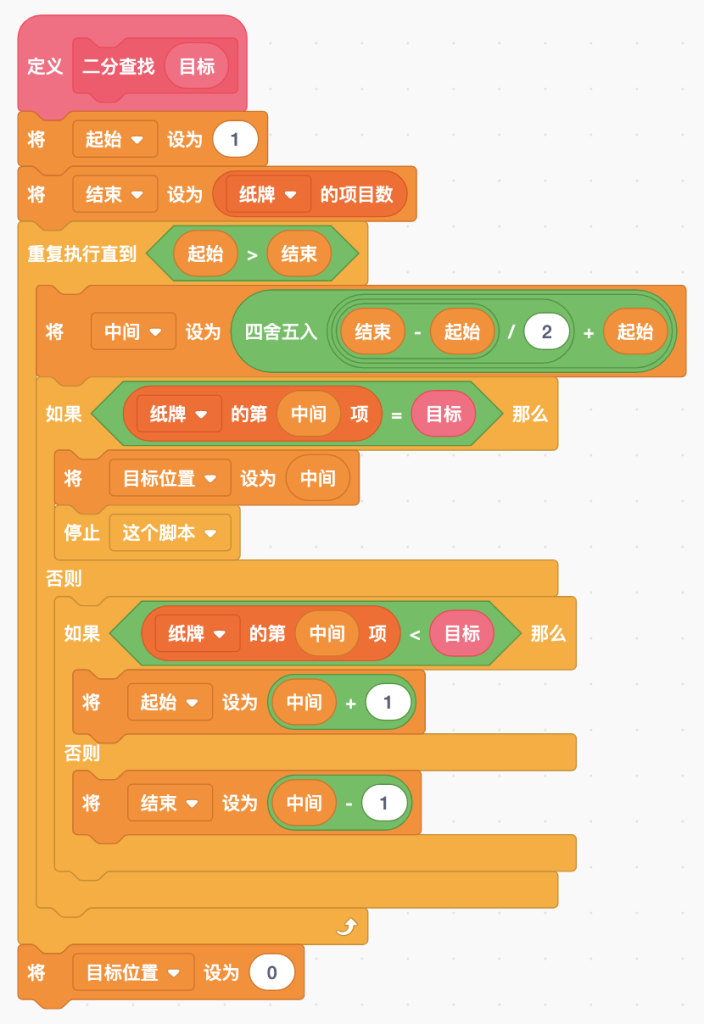
根据上面的编程思路描述,先定义“二分查找”自制积木,代码如下:
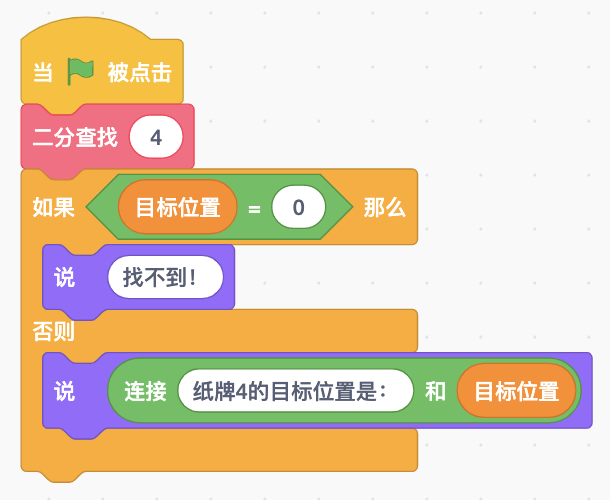
准备好纸牌列表,调用自制积木进行查找,代码如图所示:
执行程序,其效果如图所示:







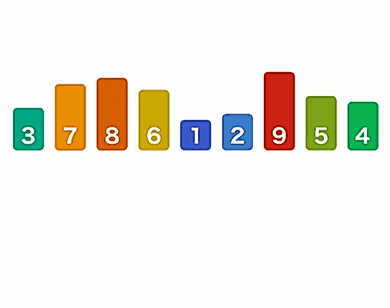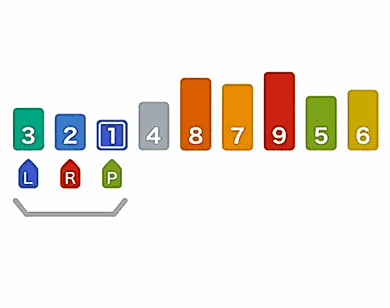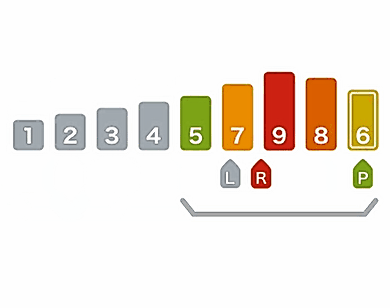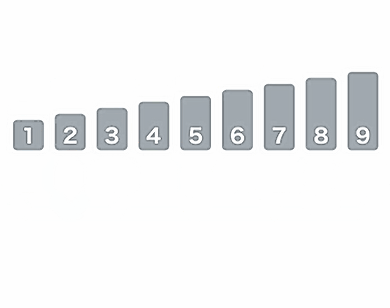







暂无评论内容