数字黑洞1和4

什么是数字黑洞1和4

前面介绍的一些数字黑洞，比如123数字黑洞、6174黑洞，都是单一数字黑洞，即经过一系列的变化最后得到一个固定的数字。而今天要介绍的数字黑洞1和4，是一个复合黑洞，所谓的复合黑洞是指由单一数字黑洞和循环黑洞两种类型组成。任何一个非0的自然数掉入这个数字黑洞中，有的会掉入数字黑洞1，之后永远是1，有的会掉入数字黑洞4，之后会一直按照“4、16、37、58、89、145、42、20”的顺序循环出现。

数字黑洞1和4的规则如下：

举个例子，取自然数129，按照上述规则进行变换，如下：

1² + 2² + 9² = 86，8² + 6² = 100，1² + 0² + 0² = 1，1² = 1 ……

最终会落入数字黑洞1中。

再比如，取自然数24，按照上述规则进行变换，如下：

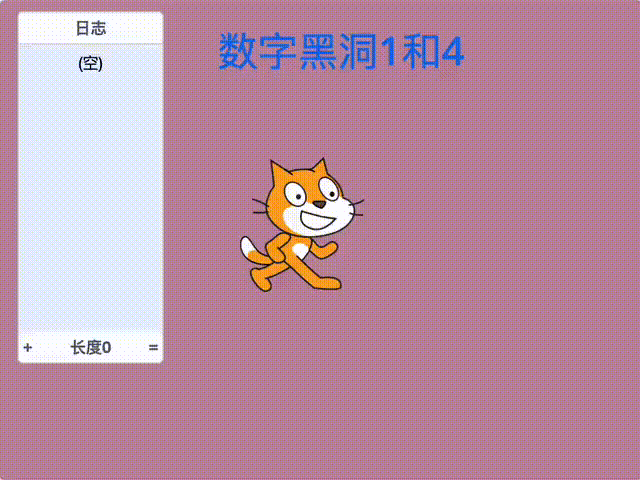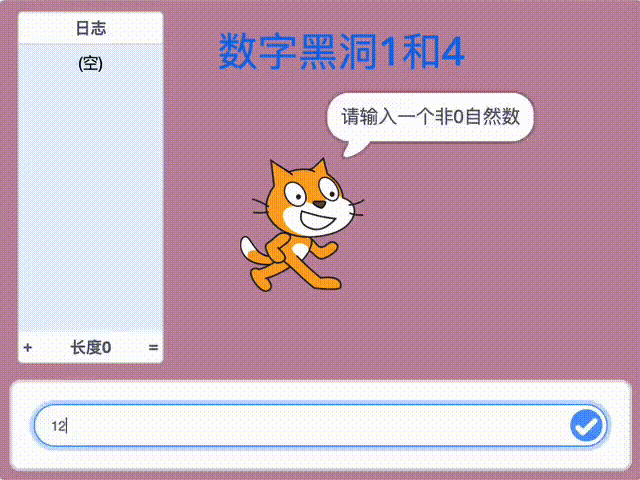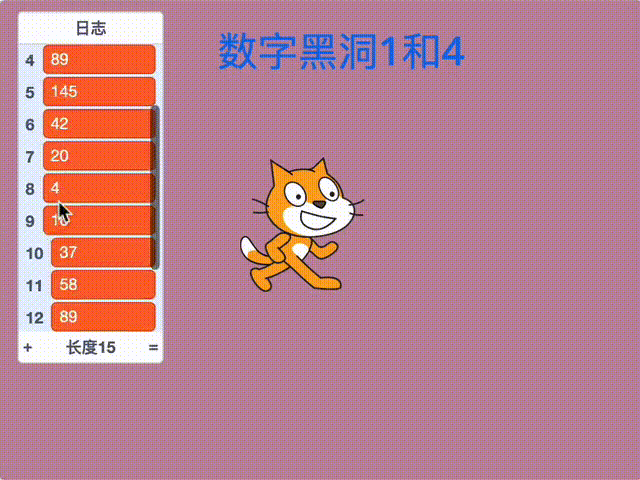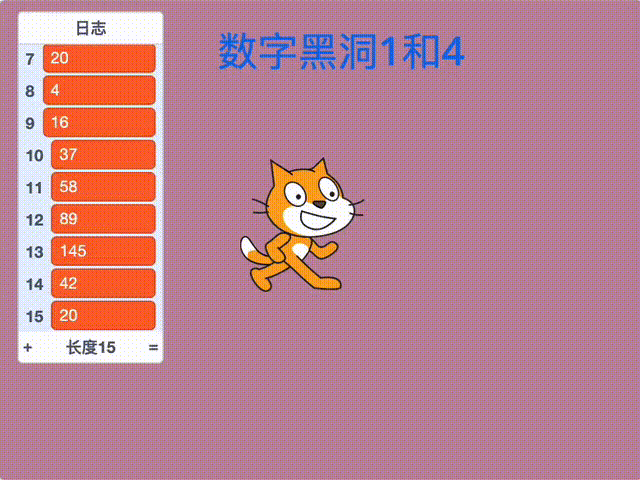
2² + 4² = 20，2² + 0² = 4，4² = 16，1² + 6² = 37，3² + 7² = 58，5² + 8² = 89，8² + 9² = 145，1² + 4² + 5² = 42，4² + 2² = 20，2² + 0² = 4，…..

最终会落入数字黑洞4的循环中。

编程思路分析

根据上面的规则描述，在验证数字黑洞时，需要分成两种情况，一是数字黑洞1，一是数字黑洞4的循环，所以这需要分开先处理，可以分别定义自制积木来实现。同时，在验证过程中，都需要拆分数字求其平方和，因此需要单独定义一个模块用于求解平方和，因此，可以将整个程序，分成5个模块：

• 求平方和：用于计算给定整数的各数位的平方和；
• 数字黑洞1和4：用于处理数字黑洞1和4，本身处理黑洞1，并在满足条件下转向黑洞4；
• 黑洞4：处理分支黑洞4
• 入口程序：获取用户输入，然后进行数字黑洞1和4的验证。

程序实现

根据编程思路分析， 分步编写代码。

1.求平方和

建立自制积木，将其命名为“平方和”，并添加参数“整数”，编写代码如下：

2.数字黑洞4

其次，添加自制积木，命名为“黑洞4”，并添加参数“整数”，编写代码如下：

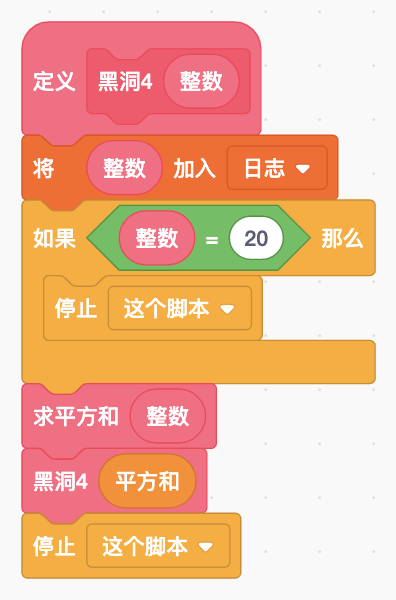
注意，为了查看求解过程，这里使用列表“日志”，将每次计算得到的数字存放到列表中。

3.数字黑洞1和4

接下来，再次创建自制积木，将其命名为“数字黑洞1和4”，并添加参数“整数”，编写代码如下：

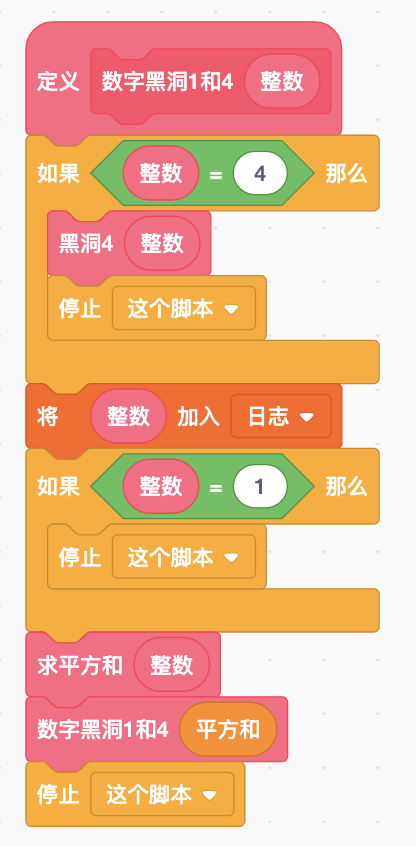
4.入口程序

最后，我们就可以编写入口程序，用于获取用户输入的整数，验证数字黑洞了，其代码如下：

作品效果

Scratch数字黑洞1和4的完整效果如图所示：