亲密数

什么是亲密数

遥远的古代，人们就已经发现某些自然数之间有着特殊的关系，亲密数就是其中的一种。据说，古希腊的数学家毕达哥拉斯曾说：“朋友是什么？朋友就是第二个我，正如220与284。”

这两个数之间有着怎样的特殊关系呢？我们来看一看:

220的因数除本身外有：1、2、4、5、10、11、20、22、44、55、110。

把220的这些因数相加：1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284。

284的因数除本身外有：1、2、4、71、142。

把284的这些因数相加：1 + 2 + 4 + 7 + 142 = 220。

看到这里，相信聪明的你已经发现了，220的所有因数之和是284，而284的所有因数之和是220。正所谓你中有我，我中有你。后来毕氏学派宣传说：人与人之间讲友谊，数与数之间也有“相亲相爱”。从此，就把220和284叫做“亲密数”，也有叫做“相亲数”或“朋友数”。

220和284是毕达哥拉斯发现的第一对亲和数。在以后的很长–段时间，不少人致力于寻找新的亲和数，但面对茫茫数海，无疑是大海捞针，虽经一代又一代人的穷思苦想，却始终毫无收获，甚至有人认为，自然数里仅有此一对亲和数。

距离第一对亲和数发现以后约2500多年，在1636年，法国数学家费马找到了第二对亲密数17296和18416。两年之后，法国数学家笛卡尔宣布找到了第三对亲密数9437506和936358。

关于亲密数，其定义如下：

如果通过手动计算来查找亲密数，这是一个巨大的工程，不过今天有了计算机和编程，要寻找亲密数就容易多了，今天我们就使用Scratch编程来找亲密数。

编程思路分析

根据上面介绍的亲密数规则，对于给定的自然数，首先需要利用枚举法计算出它的各个因素，然后将各个因素加起来，这个功能可以定义一个自制积木来实现。

其次，还是需要使用枚举法，通过自然数a，确定自然数b，再进行比较，从而得到一对亲密数。

程序实现

1.求因素之和

建立一个自制积木，将其命名为“因数之和”，添加变量“数字”，编写代码如下：

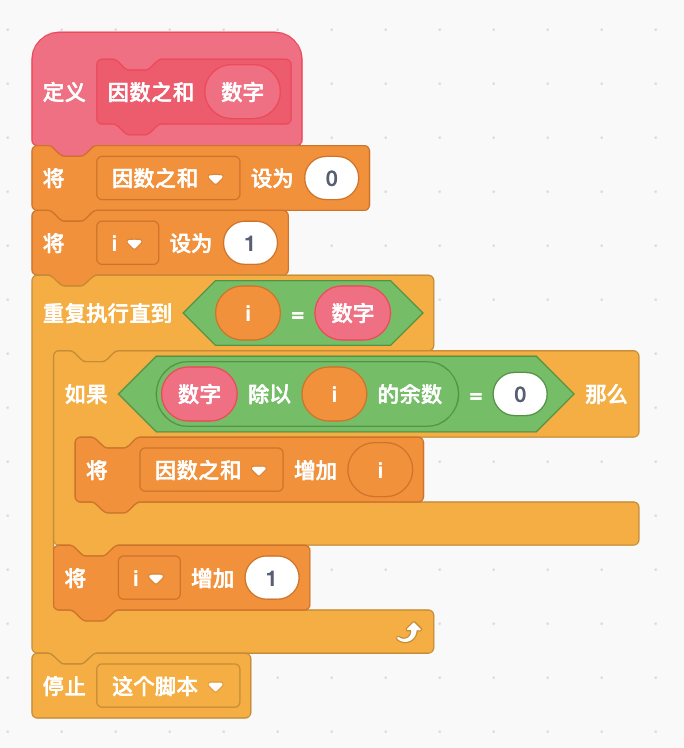
注意：这里使用了两个全局变量“因数之和”和“i”，其中i的作用是充当循环的计数器。

2.寻找亲密数

建立一个自制积木，将其命名为“亲密数”，编写代码如下：

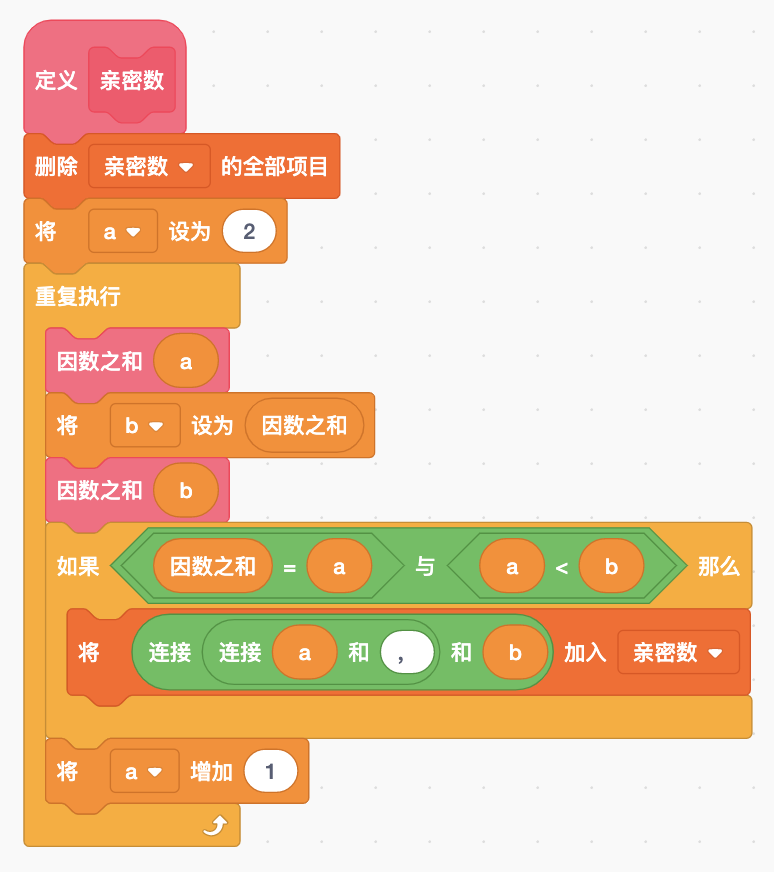
注意：这里增加了一个条件a < b，其目的是去掉完全数和重复的亲密数。比如如果a和b都等于6，a和b因素和等于6，满足条件，但是a和b相对，这是一个完全数。再比如220和284，a = 220，b = 284，它们是一对亲密数，反过来a = 284，b = 220也是一对亲密数，但是它们重复了，所以需要去掉一对。

运行效果

Scratch亲密数程序执行效果如下：

注意：运行程序，它会不停的寻找亲密数，并加入到列表“亲密数”中，越到后面，等待的时间越长，因为数字越大计算量也越大。